Méthodologie
Comment fonctionne le modèle de Depuis 1958 ? Explications techniques !
On l'entend souvent, les sondages ne sont pas une prédiction mais une capture de l'opinion à un instant donné. Mais cette capture instantanée est imparfaite. D'abord à cause de la nature aléatoire du processus d’échantillonnage lors de l'enquête de terrain, et aussi parce que l'opinion mesurée n'est pas nécessairement la même que celle qui sera exprimée le jour du vote (« ça peut encore changer »). D'autres problèmes viennent perturber la pertinence d'un sondage : le biais de sélection (le fait que les sondages représentent l'opinion… des gens qui répondent aux sondages), la méthodologie des instituts (la méthode des quotas, le rolling) et le fait qu'une partie des sondés ne répondent pas honnêtement.
L'objectif de Depuis 1958 est de prendre en compte ces incertitudes et de les transformer en une prédiction du résultat le jour du vote. Cette prédiction est probabiliste au sens bayésien. C'est à dire qu'elle reflète la quantité d'information disponible pour affirmer un résultat. En effet l'élection présidentielle est déterministe, mais c'est l'observation stochastique faite via les sondages qui est par nature aléatoire.
De plus, l'élection présidentielle en France est particulière parce qu'elle comporte deux tours. Les deux candidats du second tour sont les deux candidats arrivés en tête au premier. Mais comme les votes exprimés au premier et second tours sont issus de distributions différentes, estimer la probabilité finale qu'un candidat gagne l’élection nécessite un calcul de probabilité totale avec simulation Monte-Carlo.
Observations multinomiales
Soit \(\theta = (\theta_1, \theta_2, \ldots \theta_M)\) le vecteur, inconnu, du résultat d'un scrutin uninominal à un tour en votes exprimés. Il y a \(M\) candidats, et on a \(\sum{\theta_i} = 1\).
Un sondage idéal est un tirage :
- Issu de la population des votes exprimés
- Aléatoire (loi uniforme)
- Avec remise
Dans ce cas parfait \(\theta_i\) est la probabilité qu'un individu pris au hasard réponde en faveur du candidat \(i\). Alors les résultats d'un sondage de taille \(N\) suivent une loi multinomiale :\[ X\,|\,\theta \sim \text{Multinomial}(\theta) \]
\(X = (X_1, X_2, \ldots X_M)\) est le vecteur résultat d'un sondage, en nombres entiers de répondants. On a \(\sum{X_i} = N\), la taille de l'échantillon. En pratique, les trois critères ci-dessus ne sont pas vraiment applicables aux sondages publiés en France. On en fait cependant l'hypothèse ici. Les paramètres finaux du modèle sont adaptés de façon à maîtriser l'erreur introduite par cette simplification.
Une enquête est effectuée à une date précise, et représente donc l'opinion le jour du sondage. Pour traduire les variations temporelles, on pondère \(N\) par un facteur temporel qui dépend du nombre de jours à venir avant le scrutin. Ça n'est pas tout à fait exact, et en théorie on pourrait utiliser un modèle dynamique. En pratique c'est suffisant, car la seule prédiction intéressante c'est celle du jour de l'élection, et les calculs sont très simplifiés. \(N\) est aussi diminué pour prendre en compte la méthode des quotas, qui corrige l'hétérogénéité de la population sondée mais diminue la précision.
Inférence bayésienne
La loi de Dirichlet est l'apriori conjuguée de la loi multinomiale. Ainsi, la distribution aposteriori après observation d'un sondage est donnée par:\[ \theta\,|\,X \sim \text{Dir}(\alpha + x) \] Avec \(\alpha\) les paramètres de Dirichlet, et \(x\) la réalisation de \(X\), le sondage. Typiquement on prend un apriori uniforme \(\alpha = (1, 1, \ldots 1)\).
Ainsi, les votes exprimés sont modélisés par un vecteur aléatoire qui suit une loi de Dirichlet. La dimension de ce vecteur est \(M\) pour le premier tour, et \(2\) pour le second. Pour le premier tour, il est impossible de visualiser graphiquement cette distribution. On peut tout de même se contenter des densités marginales de chaque candidat qui sont des lois bêta.

Sur cette figure, on observe les densités marginales de résultat au premier tour. C'est à dire les chances de chaque candidat en votes exprimés, en intégrant tous les autres. Il s'agit de lois bêta de paramètres \((\alpha_i, \alpha_0 - \alpha_i)\) avec \(\alpha_0 = \sum_i \alpha_i\). Les traits noirs indiquent les moyennes. On peut faire le même exercice pour l'élection de 2012. Dans ce cas les traits rouges indiquent le résultat officiel :

Échantillonnage Monte-Carlo
Une fois \(\theta\) mis à jour avec l'addition de tous les sondages observés, on peut l'utiliser pour calculer la probabilité de n'importe quel évènement concernant le premier tour. Par exemple la probabilité qu'il n'y ait pas de second tour. Cependant, au delà de la moyenne, du mode et des paramètres des densités marginales, la loi de Dirichlet n'admet pas beaucoup de solutions analytiques. Qu'à cela ne tienne, on simule plusieurs millions de scrutins et on estime la probabilité empiriquement.
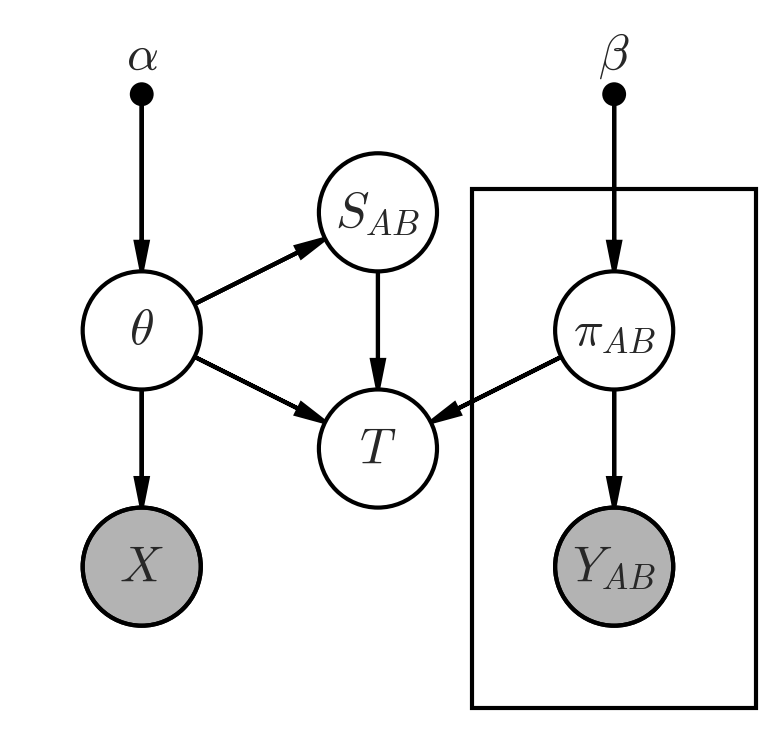
Un de ces évènements exotiques est important, c'est celui qui indique quel second tour aura lieu. C'est à dire la paire non ordonnée des deux candidats en tête. Soit donc \(S_{AB}\) la probabilité que \(A\) affronte \(B\) au second tour.
Probabilités totales
Pour être élu président ou présidente, il faut passer au second tour puis le gagner. On peut calculer la probabilité de cet évènement \(T_A\) pour chaque candidat‧e \(A\) avec une partition sur les \( M(M-1)/2 \) seconds tours possibles :